










1- Préliminaires
I- Les dessous des semi-conducteurs
1) L'atome
L'atome est à la base de la matière, vivante ou non. De diamètre de l'ordre de l'Angström (1 Ä = 10-10 m), l'atome comprend un noyau central (de diamètre mille fois plus petit), autour duquel orbitent des électrons. A son tour, le noyau se décompose en neutrons et protons, qui eux-mêmes sont constitués de quarks (10-18m).
L'électron est une particule élémentaire portant la plus petite quantité d'électricité décelable à ce jour; sa charge est e = -1.6*10-19C. Les protons possèdent également cette même quantité au signe près; leur charge est -e C. Quant aux neutrons, ils sont électriquement neutres.
L'atome est électriquement neutre, d'où Nb(proton) = Nb(électron). Ce nombre, appelé nombre quantique Z, différencie entre eux les atomes des corps purs : cuivre Cu, Zinc Zn, ... Enfin, des éléments ayant la même valeur Z, mais se différenciant par le nombre de neutrons, forment une famille d'isotopes.
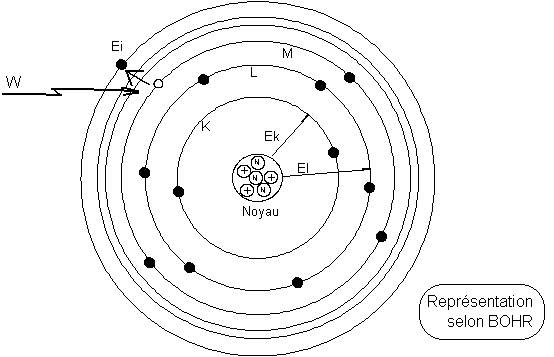
Les interactions électrons-noyau sont de type Coulombien (attraction ou répulsion entre charges électriques). La mécanique quantique a permis de proposer un modèle de l'atome. Ainsi, elle nous apprend que les électrons se placent sur des orbites ellipsoïdales centrées sur le noyau. Les orbites sont occupées de manière à ce que l'atome ait un état d'énergie minimal. En effet, chaque orbite a un niveau d'énergie propre et bien défini, qui croît avec la distance au noyau. De plus, les orbites ne peuvent contenir qu'un nombre restreint d'électrons.
Le modèle proposé est un modèle en couches. Une couche est caractérisée par le nombre quantique principal n = 1, 2, ..., en relation avec l'éloignement de la couche par rapport au noyau. Les physiciens les appellent également K, L, M, ... Sur une même couche, il peut y avoir plusieurs sous-couches ou familles d'orbites; elles sont caractérisées par le nombre quantique azimutal l : 0 <= l <= n-1. Là encore, elles portent les noms s, p, d, f, ... Dans une famille d'orbites, une orbite est repérée par le nombre quantique magnétique m avec -l <= m <= l. Enfin, chaque orbite peut recevoir deux électrons repérés par leur nombre quantique de spin.
Avec un apport d'énergie (chaleur, ...) un électron peut être excité, et capturer de l'énergie afin de passer au niveau d'énergie supérieur. Mais dès que l'apport disparaît, l'électron retourne à son état précédent en libérant l'énergie qu'il avait prise (différence entre les deux états d'énergie) sous forme de chaleur, de lumière, ...
2) Le cristal
Un cristal est un matériau formé d'atomes qui mettent certains de leurs électrons en commun pour former des liaisons de covalence. Dans un tel cas, les états d'énergie vont être modifiés par la présence des atomes voisins. Le phénomène se produit surtout au niveau des couches externes et est accentué par la distance entre atomes (appelée le pas du cristal). Chaque niveau se subdivise alors en N niveaux très rapprochés les uns des autres.
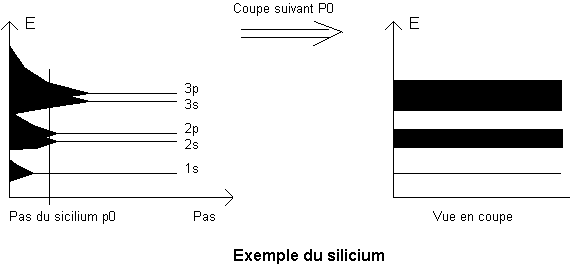
Et c'est en fonction de la dernière bande que l'on classe les matériaux isolants ou conducteurs. Si elle est partiellement peuplée à 0°K, elle s'appelle bande de conduction, d'énergie Ec, et on a un métal. Maintenant, si la dernière bande est quasiment pleine à 0°K, elle s'appelle bande de valence, d'énergie Ev, et la bande de conduction est la suivante. L'intervalle entre les deux est la largeur de bande interdite Eg. Si cette largeur est faible (<= 4eV), le matériau est un semi-conducteur, dans le cas contraire, c'est un isolant.
Les électrons d'énergie Ev participent aux liaisons de covalences, quant à ceux d'énergie Ec, ils quittent l'attraction du noyau et sont dits libres. Ainsi, dans le cas des semi-conducteurs, à température ambiante (293°K), de l'énergie thermique est communiquée au cristal et donc aux électrons de valence. Certaines liaisons vont se rompre et certains électrons vont passer à l'état libre. Là où se trouvait un de ces électrons, on trouve un trou qui va avoir tendance à attirer un électron d'une autre liaison. Ainsi, on obtient par l'application d'un champ électrique, deux modes de conduction : par électrons libres et par les trous (qui remontent en attirant les électrons voisins). Celui par électrons est plus rapide.
Les électrons tournant autour des noyaux, ces derniers sont animés de mouvements vibratoires appelés agitation thermique. On a établi une corrélation entre la température d'un corps et le degré d'agitation thermique des ses particules. Ainsi, on explique la dilatation (les atomes s'agitant davantage se repoussent les uns des autres), la fusion (les liaisons se rompent), la vaporisation (projection des atomes). Enfin, cette agitation est équivalent à un courant alternatif (bruit) qui crée des champs électromagnétiques.
3) Densité de charge - Niveau de Fermi EF
Afin de faire différents calculs sur les courants dans les semi-conducteurs, il faut étudier d'abord les densités des porteurs n (électrons) et p (trous). Pour se faire, il faut calculer en premier lieu les niveaux d'énergie possibles pour les électrons, on obtient la structure en bande. Ensuite, la fonction de Fermi f(E) donne la probabilité qu'un niveau soit occupé ou non par un électron.
f(E) = 1/(1+exp((E-Ef)/kT)), où Ef est le niveau de Fermi; il représente le plus haut niveau d'énergie occupé par les électrons à 0°K : tous les niveaux inférieurs à Ef sont alors remplis d'électrons, et ceux supérieurs sont vides.
Le calcul complet des densités de porteurs dans un semi-conducteurs suivant les théories de mécanique quantique et statistique sont :
n = A*T3/2*exp((Ef-Ec)/kT); A caractérise le matériau
p = A*T3/2*exp((Ev-Ef)/kT)
Dans le cas des semi-conducteurs intrinsèques (purs), on note Ef par Ei et en posant n = p = ni, on trouve ni = A*T3/2*exp(-Eg/(2*kT)) et Ei = (Ec+Ev)/2.
4) Semi-conducteur extrinsèque
Un semi-conducteur intrinsèque présente une grande résistance. Pour la réduire, on dope les semi-conducteurs en introduisant des impuretés qui vont créer un niveau possible pour les électrons très près de Ec ou de Ev. On déplace ainsi le niveau de Fermi en Et pour favoriser un des deux modes de conduction. Pour avoir un mode de conduction par électrons, ou de type N, on élève Et pour l'amener près de Ec. Pour favoriser les trous, ou avoir un semi-conducteur de type P, au contraire, on descendra Et pour être proche de Ev, la bande de valence. Dans ces cas, à 0°K, les électrons restent sur Et, mais dès que la température s'élève et kT devient supérieur à Et-Ec (pour un type N) ou Et-Ev (pour le type P), les transitions entre le niveau Et et la bande d'énergie voisine deviennent possibles.
Le dopage consiste à ajouter des atomes (un atome impur tous les cinq millions) qui possèdent plus ou moins d'électrons sur la couche externe. Par exemple, pour le silicium qui comporte quatre électrons sur la couche externe, on peut le doper avec du phosphore qui en a cinq : quatre seront utilisés dans les liaisons de covalence, et le 5ième sera très faiblement lié, il lui correspond un niveau d'énergie Et tel que Ec-Et = 0.012eV. A température ambiante, cet électron sera libre. L'atome qui l'a perdu prend une charge positive, on dit qu'il s'est ionisé. On dit aussi qu'un atome de phosphore dans du silicium est un atome donneur.
Maintenant, si on veut obtenir un semi-conducteur de type P à partir du silicium, on prendra pour le dopage des atomes de bore qui ne possèdent que trois électrons sur la dernière couche. Chacun de ces atomes, mélangé à du silicium, aura une liaison vacante qui va avoir tendance à capter un électron. Pour ce faire, il faut un apport d'énergie de Et-Ev = 0.01eV réalisé à température ambiante. Les atomes de bore sont des atomes accepteurs.
5) Conductivité - Courant - Diffusion
La conductivité indique la faculté de conduction du courant électrique d'un matériau. Elle est liée à la densité et à la mobilité des porteurs.
Les porteurs (électrons ou trous) se déplacent à une vitesse V proportionnelle (jusqu'à un certain point) au champ électrique E dans lequel ils sont plongés. La mobilité est définie comme le quotient V/e. On a Vn = mnE pour les électrons, et Vp = mpE pour les trous.
On peut alors écrire la conductivité x = q(n*mn+p*mp). La résistivité r est l'inverse, quant à la résistance, elle s'obtient à partir de r et de la géométrie du matériau : R = r * L/S en ohms.
Le courant électrique traversant un corps de section S s'exprime en fonction de la densité de courant J : I = S*J. Si Q est la densité de charge (nombre de charges par unité de volume), et v la vitesse des charges on a J = Q*v. Pour les semi-conducteurs, avec les deux modes de conduction, on a Jn = QnVn = Qn*mnE et Jp = QpVp = Qp*mpE. Le courant total est la somme In+Ip; il est constant dans tout le circuit. Par contre In et Ip (donc Jn et Jp) peuvent dépendre de la position dans le circuit. C'est par exemple le cas avec la présence d'accumulation momentanée de charge (jonction PN, ...). Dans un tel cas, les porteurs vont se diriger vers les endroits de plus faible concentration, générant ainsi un courant de diffusion qui se superpose au courant de conduction. Ce courant de diffusion est proportionnel au gradient de concentration des porteurs, c'est la loi de Fick : Jnd = q*Dn*dn/dx. Dn est une constante de diffusion, Dn = mn*kT/q. On peut écrire la même chose pour les porteurs de type trou : Jpd = -q*Dp*dp/dx avec Dp = mp*kT/q. Si on superpose u champ électrique E, on obtient :
Jn = Qn*mnE+q*Dn*dn/dx
Jp = Qp*mpE-q*Dp*dp/dx J = Jn+Jp
Jn et Jp de par le courant de diffusion local sont variables, par contre, J reste constant (divergence = dJ/dx = 0).
II- La diode ou jonction PN
Elle est matérialisée par le contact électrique entre un type N et un type P d'un même semi-conducteur. La jonction PN est à la base de tous les composants. Sous polarisation nulle, étant donné les concentrations de porteurs autour de la jonction, un courant de diffusion va se créer. Ainsi, peu à peu, les porteurs disparaissent à la jonction créant des ions (accepteurs Na-, donneurs Nd+). Les ions de charge opposée autour de la jonction créent le champ de diffusion Ed (avec une tension de diffusion Vd), qui s'oppose à la diffusion. Un équilibre apparaît.
Contrairement à la diffusion des porteurs majoritaires qui est freinée par le champ Ed, les porteurs minoritaires, s'ils arrivent par le procédé thermique jusqu'au bord de la charge d'espace (zone où agit Ed), ils vont être accélérés par Ed pour passer de l'autre coté, modifiant là-bas les quantités des porteurs majoritaires...
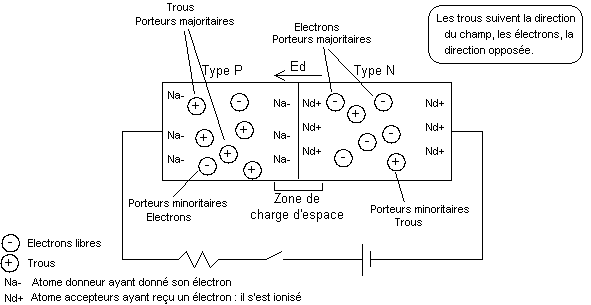
Sous polarisation inverse, le champ Ea à la même direction que le champ Ed, bloquant le passage des porteurs majoritaires. Seul un faible courant dû au porteurs minoritaires circule. Ce courant inverse dépend de la densité des porteurs minoritaires, donc de la largeur de la bande interdite et de la température.
Sous polarisation directe, Ea est opposée à Ed : on favorise ainsi le passage des porteurs majoritaires.
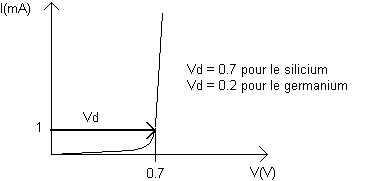
Dans tous les cas, on peut écrire J = Js*(exp(Va/(nUt))-1) avec Js ou J0, courant inverse de saturation; Ut = kT/q le potentiel thermique; n, variable d'ajustement, entre 1 et 2 en fonction du matériau, de la température et du courant. Enfin, en posant Is = S*Js, S la surface de la jonction, on a : I = Is*(exp(Va/(n*Ut)) - 1).
A partir de l'expression ci-dessus, on trouve R(V)=V/(Is*exp(v/nUt)-1) et R(I)=nUt*ln(1+I/Is)/I. Ainsi, la résistance ohmique R diminue quand V ou I augmente. De plus, la résistance dynamique rd = dv/di = nUt/I diminue quand V ou I augmente.
La température joue un rôle important qu'il faut contrôler, on trouve à I constant, dv/dt < 0, et à V constant, dI/dT > 0.
III- Le transistor bipolaire
Il est constitué par deux jonctions PN réalisées dans un même semi-conducteur. On peut ainsi avoir deux types de transistors : PNP ou NPN. Les trois broches sont appelées émetteur, base et collecteur. Dans un montage, la jonction base-émetteur doit être polarisée en direct, la jonction base-collecteur, en inverse.
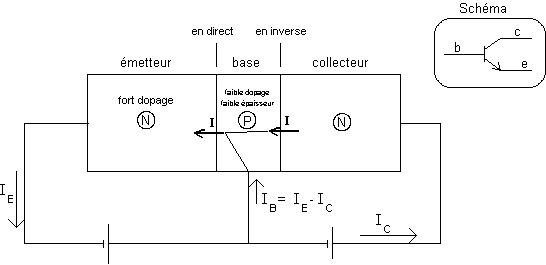
Un transistor est dit bloqué lorsque le courant Vbe < 0.7 V (Vd du silicium, 0.2 pour le germanium), ce qui correspond à la jonction base-émetteur bloquée. Il ne circule alors dans le collecteur qu'un faible courant Icb0 dû aux porteurs minoritaires.
Un transistor est dit saturé lorsque Uce atteint des valeurs très faibles, de l'ordre de 0.1 à 0.2V. Dans ce cas, le transistor ne peut plus être davantage passant. Cela correspond à abs(Vce) < abs(Vbe), c'est à dire, les jonctions b-e et b-c sont polarisées en direct.
Dans le cas général, Ic = Icb0 + a0*Ie. Où a0, qui dépend du transistor, est le gain statique en courant dans le montage base commune. Sa valeur typique est comprise entre 0.98 et 0.99. De plus, Icb0 << Ie en général, d'où Ic = a0*Ie. Avec Ie = Ib+Ic, on trouve Ic = b0*Ib où b0 = a0/(1-a0) est appelé gain en courant statique dans le montage émetteur commun; il varie entre 50 et 600.
Le courant à travers la jonction b-c, pourtant polarisée en inverse, s'explique par le dopage. De l'émetteur, fort dopé, s'échappe sous l'effet de la polarisation directe de la jonction b-e, un flux d'électrons en direction de la base. Comme la base est faiblement dopée et très fine, peu de recombinaisons sont possibles; les électrons se trouvent alors rapidement près de la jonction b-c. Or cette dernière, polarisée en inverse, facilite justement le passage des électrons vers le collecteur. C'est alors qu'apparaît le fort courant Ic.
Les caractéristiques du dopage font aussi que le courant Ie peut être assimilé au courant dû aux électrons. Celui dû aux trous étant très faible.
1) Polarisation d'un transistor
Selon la disposition d'un transistor dans un schéma, on réalise un montage en base commune, en émetteur commun et en collecteur commun.
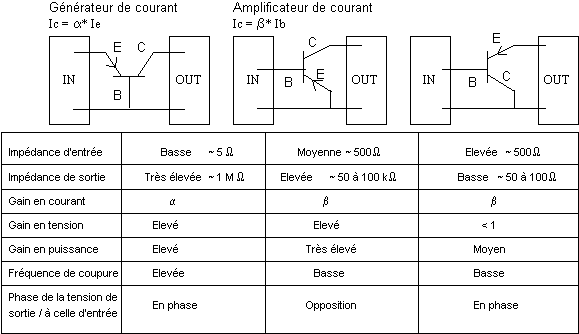
Lorsque le transistor est soumis à un réseau de tensions ou de courants continus, on dit que le point P de coordonnés (IB,VBE) est le point de fonctionnement statique. Si on superpose une composante de tension ou de courant alternatif sur les tensions ou courants continus, on va faire osciller ce point. Si l'amplitude du signal alternatif est suffisament faible, on confond l'arc de caractéristique exploitée avec la tangente à cette caractéristique en P; on dit alors que l'on est en faible signaux ou en approximation linéaire.
Calculer le point de fonctionnement statique, c'est calculer (IC, IE, IB, VCE). Pour cela, on traduit les lois de Kirchoff sur le schéma afin de trouver des équations de fonctionnement. Afin de simplifier les calculs dans des cas complexes, et pour travailler avec des signaux alternatifs, on peut remplacer le transistor par son schéma équivalent. Les deux schémas suivants sont deux représentations différentes, adaptées au mode de connexion.
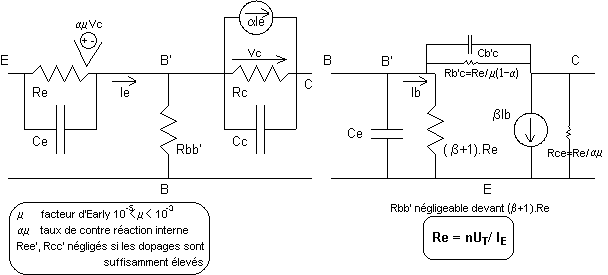
2) Les amplificateurs
Le calcul d'un amplificateur se déroule en deux étapes. La première consiste à définir le point de fonctionnement statique du transistor. Ensuite, la dernière étape regroupe le calcul des caractéristiques en régime dynamique faibles signaux.
Ainsi, on commence à calculer les grandeurs continues. Parmi elles, IE qui permet de trouver Re. Puis, on remplace le transistor par son schéma équivalent. Après avoir repérer les tensions alternatives d'entrée (Ve) et de sortie (Vs), on calcul :
- Le gain en tension Gv = Vs/Ve, ou Gv = 20*logVs/Ve pour le gain en décibel.
- Le gain en courant Gi = Is/Ie, où Is est produit dans la charge aux bornes de laquelle on receuille le signal d'utilisation.
- Gain en puissance Gp = Gv*Gi, en décibels Gv = 10*logGv*Gi
- Impédance d'entrée Ze = Ve/Ie
- Impédance de sortie Zs. Deux méthodes. Soit Zs = V1/I1 lorsque l'on attaque la sortie du schéma équivalent par V1, I1, et que l'on remplace l'entrée par son impédance. Soit Zs = Vs0/Iscc, où Vs0 est la tension de sortie à vide, Iscc le courant de court-circuit. Cette dernière méthode provient de la représentation de Thevenin.
L'electronique facile
2- LES BASES
I- Principes d'électricité
La matière est constituée de molécules. Les phénomènes mécaniques et thermiques résultent de l'action des molécules. Une molécule est composée d'atomes. Les actions chimiques et les phénomènes lumineux résultent de l'action propre de ce système planétaire ultramicroscopique.
Les électrons appartenant au noyau atomique sont à la base des phénomènes magnétiques, lorsqu'on provoque leur déplacement. Dans les mêmes conditions, ce sont les électrons libres qui sont à la base des phénomènes électromagnétiques.
L'unité de quantité d'électrons en mouvement dans un conducteur ou l'unité de quantité d'électricité circulant dans un conducteur est le coulomb. L'unité d'intensité qui est la quantité d'électricité (1 coul.) circulant dans un conducteur durant une seconde s'appelle l'ampère.
On a des bons et mauvais conducteurs : on introduit la notion de résistance spécifique ou résistivité de la matière : c'est la résistance à une température donnée d'un conducteur de cette matière ayant 1 mètre de long et 1 mètre carré de section.
La différence de potentiel (ddp) est la tension existant entre les bornes d'une source de courant à un circuit fermé, c'est à dire lorsque cette source débite. Par contre, on a coutume d'appeler force électromotrice (fem) cette même tension, mais à circuit ouvert, c'est à dire lorsque la source ne débite pas.
Le travail développé dans un circuit fait intervenir le temps, la durée de ce travail. Il correspond à la consommation d'énergie électrique.
II- La résistance
On appelle valeur nominale d'un élément, la valeur indiquée par le constructeur. Cependant cette valeur ne correspond pas exactement à sa valeur réelle. Le constructeur doit donner la tolérance de fabrication : 5%, 10%, ... De plus, afin qu'un résistance ne puisse pas posséder deux valeurs nominales distinctes, on a échelonné les valeurs de telle manière que les plages de tolérances ne se recouvrent pas. Ainsi, la série dénommée E12 correspond à une tolérance de 10%, et donne la suite : 100, 120, 150, 180, ... La série E24 à une tolérance à 5%.
Pour des écarts de température inférieurs à 200 °C, la résistance d'un conducteur varie suivant la loi : Rt = R0 * (1 + a * t) avec : Rt la résistance à la température t; R0 à 0°C; t température en °C et a = coefficient de température du matériau, toujours positif pour les conducteurs. Afin d'éviter une surchauffe qui pourrait détériorer la résistance, il est nécessaire de calculer la puissance qu'elle devra dissiper : P = U2/R = R*I2.
Le bruit d'une résistance a deux origines : le bruit thermique (électrons) qui ne dépend pas du courant, et le bruit de courant dû à son passage. Ce dernier bruit est plus fort que le thermique. Le bruit de courant dépend de la technologie. Il est très élevé dans les résistances au carbone aggloméré (5 microV/V), et très faible dans les résistances à couche métallique (0.1 microV/V).
Parmi les résistances spéciales, on a : les CTN (coeff. de temp. négatif), les CTP (coeff. positif), les VDR (selon la tension à leurs bornes), les LDR (suivant éclairage).
Le potentiomètre est construit avec une certaine loi de variation repérée par une lettre : A (linéaire), B (loga. droite), C (log. inverse), ...
La conductance est l'inverse de la résistance (1/R).
III- Accumulateur et pile
Lors de la recharge d'un accumulateur, ne jamais dépasser comme intensité de charge le dixième de la capacité de la batterie.
Dans le groupement en série, les résistances internes des éléments s'ajoutent. Cela n'a peu d'importance avec les accumulateurs pour lesquels la résistance interne est négligeable. Par contre, il faudra souvent en tenir compte dans un groupement d'éléments de piles à la résistance interne notable.
IV- Les condensateurs
On forme un condensateur en rapprochant deux conducteurs appelés armatures. Si elles sont planes, on obtient un condensateur plan. Lorsque l'on applique entre les deux armatures d'un condensateur une tension U, elles accumulent deux charges opposées +Q et -Q évaluées en coulomb. Cette capacité C = Q/U s'évalue en farads si U en volts et Q en coulomb.
Une notion importante à préciser, est la constante de temps : t = CR. Au bout du temps t, le condensateur aura atteint 63 % de sa charge totale. En cas décharge, il sera tombé à 37% de sa charge initiale. Le diélectrique d'un condensateur n'étant pas parfait, il va y avoir un courant de fuite interne à travers une résistance de fuite qui conduira à la décharge du condensateur. De même, lorsque le condensateur est soumis à une tension alternative, le diélectrique s'échauffe, agissant comme une résistance de perte Rp. Mais on préfère évaluer ces pertes par l'angle de perte d. Ainsi on obtient le diagramme de Fresnel suivant :
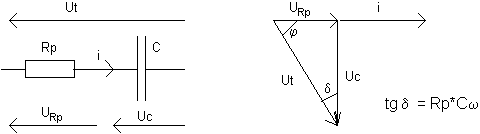
La résistance des condensateurs en alternatif (l'impédance) s'appelle la réactance capacitive ou capacitance Xc = 1/(Cw) ohms. w = 2pf est la pulsation. Si on branche un condensateur parfait sur une source de tension alternative, le courant est décalé ou déphasé en avant de 90° par rapport à la tension.
Il existe différents types de condensateurs. Les électrochimiques utilisent de l'oxyde d'aluminium pour le diélectrique : extrêmement mince. Mais le papier doit être imbibé d'acide. Afin de ne pas le détruire, le condensateur est polarisé. On trouve aussi des condensateurs au tantale dont l'étanchéité est absolue. Enfin, certains condensateurs ont un diélectrique rigide : mica ou céramique. La température influe les condensateurs au mica avec un coefficient positif, qui devient négatif pour les condensateurs en céramique.
De plus, on constate expérimentalement que l'impédance Xc de certains condensateurs augmente à partir d'une certaine fréquence contrairement à ce que laisse prévoir la formule. C'est le cas des condensateurs à électrolyte et de la plupart des modèles enroulés. Cela provient d'une inductance parasite. Ainsi dans les applications hautes fréquences, on utilise exclusivement des condensateurs plans ou monolithiques au mica ou à la céramique. De plus, on ne peut pas compter sur un chimique, même de très bonne qualité, pour supprimer les composantes HF de l'alimentation. C'est la raison pour laquelle on rencontre souvent deux condensateurs en parallèle : un chimique et un céramique. Aussi, des condensateurs spéciaux ont été étudiés pour absorber les impulsions parasites recues ou produites par certains montages : les condensateurs d'antiparasitage doivent avoir une faible inductance.
Enfin, le marquage d'un condensateur peut regrouper deux valeurs : 0.4m/500V-1500V. La deuxième correspond à une tension brève.
V- Le magnétisme
"Partie de la physique qui étudie les propriétés des aimants, des champs magnétiques."
Les forces développées par un aimant sont représentées symboliquement par des lignes, dites lignes de force, se dirigeant à l'extérieur de l'aimant du pôle nord au pôle sud. Pour lui conserver toute sa force attractive longtemps, il faut fermer le circuit magnétique : on facilite le passage des lignes d'un pôle à l'autre par une pièce en fer.
Le fer doux se laisse facilement aimanter sous l'action d'un champ. Cependant, il ne reste qu'une faible aimantation lorsque le champ disparaît; c'est le magnétisme rémanent.
Le maintien d'un champ n'exigent fondamentalement aucune dépense d'énergie. L'énergie dépensée dans les électro-aimants vient de la résistance du fil.
L'intensité d'un champ magnétique H caractérise le nombre de lignes de force traversant une surface unité perpendiculaire à celle-ci. Elle se mesure en ampère par mètre (A/m). Le total des lignes sur une surface S est le flux magnétique (Þ), mesuré en weber. On a Þ = CM * S * µ0 (µ0 = 4Ò10-7).
L'extrémité de l'aiguille aimantée, d'une boussole, indiquant le nord géographique s'appelle le pôle nord de l'aimant.
VI- L'électromagnétisme
"Ensemble des interactions entre courants électriques et magnétisme"
Un courant électrique circulant dans un conducteur engendre un champ magnétique autour de ce conducteur qui peut être mis en évidence par une boussole (règle du tire bouchon). Cette création de champ par un fil conducteur est à l'origine de certains problèmes avec des ampli. à gain élevé.
Lorsque l'on désire un champ intense, on enroule le conducteur en bobine. Le champ est proportionnel au nombre de spires, mais aussi à l'intensité les parcourant : la notion d'ampère-tour est donc une caractéristiques importante d'une bobine. Si on introduit à l'intérieur d'une bobine une barre en fer, elle est aimantée par le champ (elle est le siège d'une induction magnétique). En fait, elle canalise les lignes : elle est appelé noyau magnétique et sa polarité est obtenu par la règle de tire-bouchon. L'augmentation des lignes de force est conditionnée par la qualité magnétique du métal constituant le noyau. Cette qualité s'appelle la perméabilité du noyau µr; la perméabilité magnétique est µ = µr(sur tables) * µ0 (dans vide).
L'induction magnétique ß est donc le nombre de lignes de force par mètre carré de section du noyau, s'exprime en teslas ( = 10^4 gauss).
Le flux d'induction est alors Þ = ß * S = µr * h * S. ß peut contenir le coefficient multiplicateur cos theta, si l'induction n'est pas perpendiculaire à la surface. h représente l'intensité du champ magnétique en ampère-tour par mètre.
Un noyau supporte un certain nombre de lignes au delà duquel il est saturé. Lorsque l'on veut aimanter une barre de fer sous l'action d'un champ, on constate que les intensités d'aimantation ne suivent pas la même courbe lorsque l'on change le sens du champ : les intensités restent en retard sur les valeurs précédentes : c'est le phénomène d'hystérésis.
L'hystérésis est dû à la résistance qu'offrent certaines matières à la désaimantation (force coercitive); cette résistance donne lieu à une perte d'énergie qui se transforme en chaleur : perte par hystérésis. Elle est proportionnelle à la surface embrassée par le cycle d'aimantation.
Le phénomène d'aimantation est réversible : toute variation de flux magnétique à l'intérieur d'un circuit provoque une force électromotrice proportionnelle à la variation de flux dans l'unité de temps, et le sens de cette force électromotrice induite est tel que le courant tend à s'opposer à la variation du flux inducteur.
Les courants induits ne se produisent pas uniquement dans un enroulement secondaire couplé à l'enroulement inducteur, mais également dans toute masse métallique soumise aux variations du flux : ces courants induits indésirables portent le nom de courants de Foucault.
Tout bobinage parcouru par un courant I produit un flux magnétique à travers chacune de ses propres spires. La somme des flux traversant toutes les spires s'appelle le flux propre; il est proportionnel à I : Þ = L * I. L est le coefficient de self-induction, il représente la propriété d'une bobine de s'induire elle-même. Son unité est le henry (H), et est le coeff. de self-induction d'une bobine lorsqu'une variation de 1 A de l'intensité qui la traverse en une seconde provoque une fem induite de 1 V.
Pont de Wheatstone : 4 résistances montées en losange; lors de son équilibrage (r1/r2 = r3/r4), l'intensité circulant dans la diagonale est nulle. Lois de Kirchhoff : somme des courants à un noeud = 0 (loi des sommets) et la variation totale du potentiel le long d'un contour est nulle (loi des contours) .
I- CHARGE ET COURANT
Les conducteurs dont il va être question sont composés d'ions et d'électrons. Dans les conducteurs solides, les ions sont fixes; dans ce fluides (plasmas, électrolytes) les ions et les électrons sont mobiles.
Pour un type de particule de charge 'e' :
* densité numérique électronique
n = lim v->0 ( N*e/ v)
* densité de charge :
ro(r) = lim v->0 ( N(nbre ds v)*e/ v (centre sur r)
* densité de courant
j(r) = lim v->0 ( J/ v) = ro(r)*v(r)
Rque : J = N*e*v(r) (courant des particules de v)
Avec plusieurs types différents :
ro(r) = õ roi(r)
j(r) = õ ji(r)
Equation de continuité :
Soit dI = j.n*dS Charge traversant dS par unité de temps vers n
I = ¶ sur S
§ j.n*dS Charge traversant S = COURANT
Alors
Ùro/Ùt + div(j) = 0
Savoir aussi :
Va-Vb = E.AB
Les électrons participant à un courant de 1 A se déplacent à une vitesse < 1mm/s. C'est grâce au champ électrique qui s'établit à la vitesse de la lumière que l'effet se fait sentir à distance.
II- PHENOMENES STATIQUES
1- ELECTROSTATIQUE
"Science qui étudie les propriétés des corps porteurs de charges électriques en équilibre"
* Force de Coulomb (ou électrostatique) créé en r par N charges :
F(r) = eE(r) (force sur charge e en r)
* Champ électrostatique :
E(r) = õ de 1 à N (ei*(r-ri)/(4*Ò*¯0*(r-ri)^2))
* Loi de Gauss (forme locale)
div E = ro/¯0
rot E = 0
* Energie électrostatique d'un système à N charges (pour les envoyer à l'ý)
Travail pour reformer un système à n électrons depuis l'infini
W = 0.5*õ i,j de 1 à N, i <> j (ei*ej/(4*Ò*¯0*(r-ri)))
¶ sur R^3
W = ¯0*0.5*§ E^2(r)dv
* Potentiel électrostatique (scalaire)
L'énergie du système de 2 charges devient e*V(r0)
V(r) = õ de 1 à N (ei/(4*Ò*¯0*(r-ri)))
On a :
E = -grad V
V = -ro/¯0 (nabla = div grad)
et
W = 0.5*õ de 1 à N (ei*V(ri))
¶ sur R^3
W = ¯0*0.5*§ E^2(r)*dv
* Forme intégrale (loi de Gauss) :
¶ sur S
§ E.n*dS = Qint/¯0 qq soit S fermée, Q champ intérieur à S
¶ sur C
§ E.dl = 0 qq soit C contour fermé
2- MAGNETOSTATIQUE
* Force de Lorentz : action d'un champ magnétique sur un électron mobile. La force de Laplace est la conséquence de celle de Lorentz sur un fil parcouru par un courant.
* Force de Laplace (N circuits ci parcourus par N courants ii) :
F(r) = e*v ^ B(r) force sur e en r à vitesse v
Cette force ne travaille pas, car perpendiculaire à v.
* Champ de Laplace : ¶
B(r) = õ de 1 à N (µ0*ii/4/Ò*§ (dri ^ (r-ri))/(r-ri)^3)
* Loi d'Ampère (forme locale)
rot B = µ°*j
div B = 0
* Potentiel vecteur (magnétostatique)
¶ sur R^3
A(r) = µ0/4/Ò * § j(r')/(r-r')*dv'
On a :
div A = 0
B = rot A
A = -µ0*j (nabla)
* Loi d'Ampère (forme intégrale)
¶ sur C
§ B.dl = µ0*Iint qq soit C fermé, Iint courant dans C
¶ sur S
§ B.n*dS = 0 qq soit S fermée
L'electronique facile
3- LE RESTE
I- Les dessous des semi-conducteurs
1) L'atome
L'atome est à la base de la matière, vivante ou non. De diamètre de l'ordre de l
REMARQUES INFORMATIQUE
Le retour horizontal du faisceau du tube cathodique dure 4 micro secondes environ. Quant au retour vertical, il est de l'ordre de 7 milli secondes.
Pour nous contacter : siteclic.aro.microclic.com en remplaçant '.aro.' par @
3 requêtes